Revue CréAtions en ligne "Art et maths" n° 184- octobre 2007 - SOMMAIRE
| CréAtions "Arts et maths"
Revue en ligne annoncée dans le Nouvel Educateur n° 184 Publication octobre 2007 |
Édito - Art et math - Nouvel Educateur n° 184
 |
Revue en ligne CréAtions n°184 "ART ET MATHS" Édito |
|
Art et maths
Dans ce numéro de CréAtions, le comité de rédaction a voulu montrer qu’on pouvait, dans notre pratique de tous les jours, faire des ponts et autoriser des liens entre l’art et les mathématiques, pour permettre à l’enfant « d’accéder au statut d’auteur en math comme en art » (Danielle Thorel), en développant l’exercice de sa créativité. Dans les articles de ce numéro intitulé ARTS ET MATHS, le lien avec les maths est révélé le plus souvent par la présence, dans les productions d’enfants, de formes géométriques et par le recours à la terminologie mathématique, lors des moments de verbalisation et de présentation des productions à la classe, selon une approche qui se veut globale. Fait-on pour autant des maths au sens strict du terme ? Nous ne le pensons pas. Nous sommes sur ce point d’accord avec l’article de Rémi Jacquet paru dans le Nouvel Éducateur de février 2010, intitulé « Création artistique, création mathématique », dans lequel il rappelle que si l’émotion esthétique peut servir de ressort à l’apprentissage, par exemple dans une activité de traçage de rosaces qui nous émerveillent, l’apprentissage des mathématiques suppose la construction d’un langage et d’une démarche proprement mathématiques. C'est la raison pour laquelle, dans cet article du numéro ARTS ET MATHS, il n’est pas question pour nous de prétendre décrire une séance de mathématiques. De son côté, l’apprentissage de l'art suppose la construction d’un langage et d’une démarche proprement esthétique qui inclut la mathématique comme forme symbolique. Dans la rosace, l'émerveillement dont parle Rémi vient de la coordination des deux langages. Il nous semblait important, en créant ce numéro et en le rangeant sous « la rubrique Maths », de souligner l’intérêt « d’entrer » en mathématiques par l’activité artistique, conscients de ne pousser que la porte de l’antichambre! Selon nous, l’apprentissage devrait même débuter ou déboucher sur une production artistique, pour justement mettre les enfants en condition d’aiguiser leur regard et leur geste, de les rendre attentifs à une lecture mathématique possible du monde (faire des correspondances, comparer, réinvestir des savoirs, etc.); et ce en aval ou en amont des séances de créations mathématiques prévues pour : « développer la faculté à voir les mathématiques dans les objets et le monde, à entrevoir, prévoir, imaginer de nouveaux liens, de nouvelles relations entre ces objets, de nouvelles solutions. » (Rémi Jacquet). En choisissant de laisser le référencement des articles de ce numéro sous la rubrique « maths » ou "géométrie", nous tenions à apporter cette précision nécessaire afin d’éviter les confusions. A l’époque de la publication de ce numéro, la question du référencement des articles selon des rubriques n’existait pas encore. Cette question se pose à présent sur le site. Nous espérons avoir clarifié les choses. |
Sentier artistique et géométrique
 |
Revue en ligne CréAtions n°184 "Art et Maths" Classes de 5ème, Collège Jules Vallès, Fontaine (Isère) - Enseignantes : Anne Voltolini et Emmanuelle Heidsieck |
|
Sentier artistique et géométrique
Land-Art au collège - Invention dans un parc
La sculpture est un art imaginaire
Art éphémère ou art de pierre
Naturel ou fantastique, tout est dans l’air ou sur terre
De l’invention à l’assemblage je réfléchis en solitaire
Art nouveau ou art de l’eau, feuilles ou bien murs de pierres
Rudimentaire ou développée la construction se fait d’avant ou de notre ère
Tout pour dire que la sculpture est un art artistiquement extraordinaire.
  Symétries et formes
Lors de la troisième séance, chaque groupe de deux ou trois élèves doit réaliser un croquis précis et détaillé en décrivant les matériaux prévus pour sa première installation de Land Art. Différentes contraintes mathématiques sont imposées : "Dans votre installation on doit voir : Pour aider les élèves à construire leur projet, on peut leur donner des incitations telles que : "C’est la répétition qui fait ma valeur", "Enrouler, dérouler, construire", etc. Les élèves doivent aussi estimer les dimensions de leur œuvre et lui donner un titre. Lors de la séance suivante, les élèves arrivent au parc en possession de leur projet. C’est un vaste parc, peuplé d’arbres anciens et de bambous, traversé par un ruisseau. Ce lieu reste très naturel. De grandes étendues d’herbes alternent avec des zones boisées. Il n’y a pas de massif de plantations, les fleurs sont toutes sauvages. Cet endroit très riche permet une multitude de réalisations : en automne, les feuilles colorées, les marrons, les écorces et au printemps, les pissenlits, les crocus et autres fleurs. Les élèves peuvent exploiter les milieux secs et humides, le ruisseau, la forêt de bambous, les pierres, les branches, etc.
|
Atelier à l'espace de l'Art concret à Mouans-Sartoux (congrès de Valbonne)
 |
Revue en ligne CréAtions n°184 "ART ET MATHS" Témoignages de congressistes - Congrès de Valbonne - Août 2005 |
|
Atelier à l'espace Art concret de Mouans-Sartoux Découvrir des dispositifs libérateurs - Vivre les ateliers pédagogiques
Il me semblait important d’intégrer ces animatrices à nos travaux car je sentais émerger, à chaque intervention pour ma classe, des "liens" au niveau de l’expression, de l’ "apprendre à regarder", de l’appréhension du monde…Le secteur Créations s’est greffé sur cette idée pour la faire évoluer et la travailler avec les médiatrices, afin de lui donner la forme que les congressistes ont connue. Apparemment, tous ceux qui ont vécu les ateliers proposés pour le congrès en ont retiré pas mal d’informations, « scolaires » ou plus personnelles. Des réflexions sont en marche…
Un espace riche de possibles Créé par deux collectionneurs, Sybil Albers et Gottfried Honegger, ainsi que le maire de Mouans-Sartoux, André Aschieri, inauguré en 1999, l’Espace de l’Art Concret défend les enjeux d’un projet artistique et culturel lié à l’éducation du regard. L’Espace articule son action artistique, culturelle et éducative autour de trois pôles complémentaires :
Témoignages
Des dispositifs libérateurs
Merci à Sandra, Régine et Brigitte pour leur accueil et leur disponibilité. Merci aussi à Nadine, au GD 06, au chantier CréAtions et à la ville de Mouans-Sartoux d’avoir permis ce moment d’envol culturel.
|
Adopter un jardin
 |
Revue en ligne CréAtions n°184 "ART ET MATHS" I.M.E., l’Isle Adam (Val d’Oise) - Intervenant : Xavier Boggio, plasticien |
|
Adoptez un jardin Création de flaques de résine colorées au cœur du jardin du Château d’Auvers sur Oise
Origine du projet
En 1996, le ministère de la Culture avec les ministères de l’Education Nationale, de l’Environnement et de l’Agriculture lance une opération intitulée "Adoptez un jardin".
|
Tisser des liens entre les mathématiques et les couleurs
 |
Revue en ligne CréAtions n°184 "Arts et Maths" Classe de CE2/CM1, école publique, Bonneveine 2, Marseille (Bouches du Rhône) - Enseignant : Jean-Noël Manouba |
|
Tisser des liens entre les mathématiques et les couleurs
Intersections de couleurs et résolutions de problèmes
Les couleurs nous entourent de toutes part. Elles alimentent notre perception, nourrissent notre sensibilité au monde et forgent notre sens symbolique. Elles agissent directement sur l’affectif. Les mathématiques, quant à elles, favorisent la conceptualisation et le raisonnement logique (formulation d’hypothèses, vérifications). Elles sont davantage de l’ordre du conceptuel et du rationnel. Elles entrent dans notre vie par la voie de l’école et du travail. Existe – t - il cependant, et malgré ces apparentes oppositions, des liens entre « mathématiques de l’homme » et « couleurs du monde » ? Quels tissages pourrait-on créer ?
Récemment dans l’histoire de l’humanité, l’homme s’est servi indirectement des mathématiques pour modéliser des couleurs grâce à l’outil informatique. C’est donc que la production de couleurs artificielles a besoin de mathématiques. Inversement, aujourd’hui, les mathématiques pourraient-elles avoir besoin des couleurs ? Par exemple, les concepts mathématiques pourraient-ils être davantage circonscrits et ainsi davantage compréhensibles grâce à une approche basée sur les couleurs ? Un premier usage des couleurs en classe de mathématique est déjà celui des éditeurs scolaires qui proposent aux enfants du cycle 2 des exercices de « coloriage » utilisant un codage des couleurs. A chaque couleur est associé un nombre et il s’agit alors de calculer correctement des sommes pour trouver la couleur que l’éditeur a choisie pour chacune des parties (toutes juxtaposées) du dessin. Rien de bien créatif jusqu’ici, l’intérêt étant pour l’enfant qu’un coloriage juste permette parfois de découvrir ce qui se cache derrière une multitude de traits et de chiffres comme dans le très ancien jeu des points liés. Intersections de couleurs et résolutions de problèmes
La production d'un élève après que le processus de traduction des couleurs en nombre et puissance ait été mis en évidence en classe entière.
Commutativité/associativité
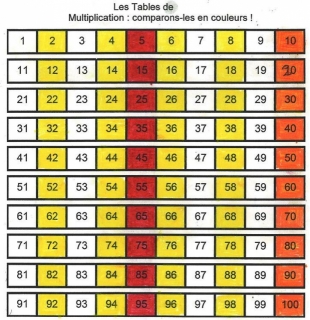
Il en résulte alors un certain nombre de principes que l’action mathématique correspondant au mélange de couleurs devrait vérifier. Cette action doit être commutative. En effet, mélanger du bleu et du jaune ou du jaune et du bleu est équivalent. Cette action doit être associative. En effet, lorsque je mélange trois couleurs, je peux en mélanger deux puis ajouter la troisième ou bien mélanger les trois en même temps. Arrêtons-nous là ! : l’addition et la multiplication semblent déjà toutes deux convenir. Cependant, il n’est pas difficile de se rendre compte que la multiplication convient ici davantage que l’addition. Imaginons en effet que l’addition convienne. Le nombre 6 représenterait alors une couleur qui puisse être obtenue à l’aide des mélanges de 5 et 1, de 4 et 2 ou de 3 et 3. La couleur du 6 serait le résultat de mélanges divers pouvant être obtenus avec les couleurs des nombres 1, 2, 3, 4, 5 et 6. En généralisant, toute couleur (codée par un nombre n) « contiendrait » toutes les couleurs la précédant (n-1, n-2,…/… 2, 1) : on ne pourrait alors, et par exemple, jamais obtenir deux des trois couleurs primaires, ce qui ne nous conviendrait pas. La multiplication en revanche permet de garder une trace des nombres (et donc des couleurs) par lesquels elle se réalise via une certaine forme de codage. Ainsi, si on associe au jaune le nombre 2, au bleu le nombre 3 et au rouge le nombre 5, on obtient un système de représentation des couleurs permettant d’obtenir tout le cercle chromatique en considérant les multiples de 2 (contiennent au moins une couche de jaune), de 2m (contiennent davantage de jaune), de 3 etc. La question de l’utilité d’une telle mathématisation du graphisme coloré se pose alors. Nous laissons au lecteur le soin de réfléchir à toutes les possibilités offertes par un « milieu » où nombres et couleurs seraient tout autant régis par les règles de la chromatique que par celles de l’arithmétique PGCD (plus grand commun diviseur) et PPCM (plus petit commun multiple) ; notamment voir ci-après. Cela permettrait - il aux enfants de mieux comprendre les couleurs ? Les nombres ? les deux ? aucun des deux ? En réponse à l’analyse du deuxième cas (ci - avant), on peut émettre l’hypothèse que le domaine numérique permet une discrimination plus fine des couleurs, évitant ainsi de fastidieuses recherches de couleurs. La table de Pythagore (et ses variantes) donne d’ailleurs une clé de passage des nombres aux couleurs et inversement (coloriée comme ci - dessus dès septembre 2001, dans une classe coopérative de CE2, à Marseille).
Lisa et Garance réussissent une distinction non équivoque (séparation complète des couleurs et distinction entre les différentes puissances comme autant de bandes d'une même couleur).
On peut montrer que, finalement, il suffit de considérer les nombres (2m x 3n x 5p).pour obtenir toutes les couleurs du cercle chromatique. Inversement, on remarque alors que l’on ne peut pas atteindre tous les nombres entiers naturels par une telle modélisation. Pensez à 7 par exemple ! A cet égard, parler de la décomposition de couleurs en couleurs de bases se transpose mathématiquement au niveau du codage d’un nombre par les nombres premiers. L’unicité d’une couleur obtenue à partir des mêmes quantités de peintures de base coïncide alors au niveau mathématique à l’unicité de la décomposition en facteurs premiers des entiers naturels. Par exemple, il existe trois façons de mélanger deux doses de bleu (32) et une dose de jaune (21) : tout est mélangé en même temps (18x1 ou 1x18), les deux doses de bleu (32) sont associées à la dose de jaune (21) ou encore, une dose de bleu et une dose de jaune sont d’abord associées (3x2) puis sont mélangés à une dose de bleu. On retrouve bien les différentes décompositions de 18 en produit de deux facteurs (18 = 18x1 = 9x2 = 6x3) et il y a concordance entre l’unicité de coloration du mélange final (quelque soit l’ordre de mélange) et l’unicité de décomposition de 18 en facteurs premiers élevé de leur puissance (18 =21 x 32 ). Se réconcilier avec les mathématiques
Il est alors possible d’exploiter un tel système dans des activités très variées et de tout âge, à tout moment. Une telle démarche peut aider à concilier ou à réconcilier les enfants avec les mathématiques d’une part et avec la résolution de problème d’autre part, celle-ci étant trop souvent considérée comme l’apanage des mathématiques, dont elle ne constitue, encore aujourd’hui, pourtant pas assez souvent le cœur. On propose ci-après deux exemples (figures a et b) à résoudre mathématiquement et/ou par une recherche de couleurs (cas valorisant les points de vue symétriques de PGCD et PPCM ainsi que deux autres (figures c et d) qui peuvent être à « mathématiser ». - la figure (c) est « résolue » en couleurs. - La figure (d) peut avoir la figure (c) comme solution mais possède une autre solution en couleurs et donc une autre solution mathématisée (que nous laissons à la sagacité du lecteur).
Une question mérite ici d’être posée : la mathématisation des couleurs peut-elle favoriser une coloration des mathématiques ?
|
François Morellet, un artiste contemporain.
 |
Revue en ligne CréAtions n°184 "Arts et Maths" François Morellet, artiste |
|
François, Morellet, un artiste contemporain dont le travail est étroitement lié aux mathématiques
Dans notre article précédent nous avions voulu montrer que l’enseignement des mathématiques, tel que nous le souhaitions en classe, n’était pas très éloigné de la démarche artistique et qu’il pouvait être porteur d’émotions esthétiques, de sensibilité et de créativité.
Pour nous permettre de continuer notre propos, nous présentons ici un artiste contemporain dont le travail est étroitement lié aux mathématiques. François Morellet est un artiste français né en 1926 qui cherche à évacuer de ses œuvres toute trace de subjectivité. Ses travaux abstraits ne semblent dépendre que de "systèmes" combinatoires. Les lignes et les courbes, pour se multiplier, obéissent à des "décisions mathématiques" de l’artiste ou au hasard de listes de nombres comme par exemple les décimales de pi ou les chiffres d’un annuaire téléphonique. Morellet vise à réduire au minimum le sens de l’œuvre d’art.
Dans cette autre œuvre "Л puissant n° 4-1=30°-13 décimales", Morellet fait varier les angles de ses bandes adhésives en suivant les chiffres des décimales de Л. Il déclare dans les années 70 : "En effet, si depuis 1950, mes œuvres flirtent avec le vide, c’est avec cette espèce bien particulière de vide dû à l’absence de "nature". Absence voulue de toute évocation de la "nature", de toute justification "naturelle", de tout principe naturel. Et bien, une justification de ces œuvres "dénaturées" c’est d’être en accord avec un monde comme je le conçois," dénaturé" lui aussi, débarrassé de Dieu et de son résidu: l’idée de «nature». C’est d’accepter un monde régi par le hasard et l’artifice, d’accepter un présent qui n’est plus refusé au nom d’un passé perdu ou d’un avenir à instaurer. C’est de tenter de réaliser un art "artificialiste" qui est aussi éloigné de l’art naturaliste que celui-ci a pu l’être de l’art sacré." Pourtant, de ces œuvres ne surgit-il pas une élégance, une pureté, une énergie? Toute cette complexité, ces chemins qui se croisent au hasard, ces rencontres fortuites, n’est-ce pas la vie même ?  Ce "Л cheminement" ne nous fait-il pas penser aux traces d’un animal affolé? au chemin d’une vie faite d’errance, de brusques changements de direction remis en cause aussitôt? Sommes-nous nous aussi prisonniers d’un système, de notre destinée? Y a t-il quelque chose d’inéluctable dans notre propre cheminement?
François Morellet s’est aussi intéressé au dialogue entre l’architecture et l’œuvre d’art. "Ce qui m’intéresse à l’heure actuelle serait plutôt une désintégration architecturale. C'est-à-dire trouver un autre rythme que celui de l’architecture et jouer avec les interférences de ces deux rythmes. Mes interventions ne plaisent pas aux architectes en général parce qu’elles semblent ignorer leurs esthétiques et les structures de leurs constructions. C’est normal puisque l’œuvre même consiste en un combat de deux structures: la leur et la mienne." La brutalité de cette œuvre, intitulée avec humour "La défonce" (elle se trouve à La Défense) témoigne de son attrait pour la provocation et de son penchant pour la destruction. Une barre métallique, tel un pieu, transperce le bâtiment pour lequel elle a été créée. Elle déstabilise notre regard et fait tanguer les hautes tours de La Défense. Dès les années 60, Morellet utilise les néons dans son œuvre. "Les néons m’ont beaucoup occupé. C’est un matériau dur et froid qui me permet d’utiliser le temps et le rythme. On a compris qu’avec la lumière électrique, on pouvait obtenir une lumière constante et contrôlable. C’est un premier stade. […] Le second stade pour les artistes fut de jouer avec cette lumière comme leurs prédécesseurs l’avaient fait avec la lumière du jour. Nous arrivons maintenant à un troisième stade, c’est la source lumineuse elle même qui doit être considérée comme matériau plastique et non son reflet." Dans ces installations, Il fait intervenir le spectateur qui programme l’allumage des néons. Il supprime à l’œuvre d’art son caractère immuable et définitif. L’artiste n’impose plus un moment privilégié qu’il a arbitrairement choisi; il propose une série de situations qui se développent en dehors de lui. "La participation du spectateur à la création et à la transformation de l’œuvre d’art est sans doute la conception la plus éloignée du créateur tout puissant romantique. Les génies arbitraires, dont le 19ème siècle a fabriqué les légendes s’effacent devant le spectateur."
Dans les années 90, il entame la série des lunatiques, intitulées "lunatiques néonly". Ces formes rondes sont une référence à la lune et à son influence sur les comportements. Une spirale inscrite dans le cercle de départ constitue une grille qui sert de points d’appui aux arcs. Les segments de cercle, cette fois ci, obéissent aux chiffres aléatoires de l’annuaire du Maine et Loire comme dans la série "des relâches". Certains chiffres servent à déterminer les points d’appui sur la spirale et d’autres leur inclinaison.
Pourtant ces segments de cercle "obéissants" nous apparaissent au contraire indisciplinés, effrontés, frivoles, chahuteurs , épris de liberté, s’échappant même de leur "cercle cage" poussés par leur énergie lumineuse. Ce détachement par rapport aux œuvres d’art habituellement réalisées, nous l’avons trouvé chez certains enfants qui ont pris goût à composer des dessins «obéissants». Ces enfants issus d’un milieu difficile prennent un énorme plaisir à se donner des règles dans leur composition, eux qui ont bien du mal à se donner des règles quand ils sont livrés à eux mêmes dans leur quartier. Cette recherche de régularité, de netteté dans les traits, de précision dans la réalisation est-elle le reflet de leur quête de repères, de système de valeurs qu’ils cherchent parfois désespérément dans leur famille, dans la religion, à l’école ? Ou est-ce la peur de s’exprimer, peur qu’on les découvre ? Un refuge pour éviter la mise à nu ?
|
James, deux ans de création-recherche en maths
 |
Revue en ligne CréAtions n°184 "ART ET MATHS" Cycle 3, école de Toreille, Vence (Alpes Maritimes) - Enseignant : Jean-Charles Huver |
|
James, deux ans de création-recherche en maths James a effectué son cycle 3 dans deux classes Freinet de l’école Toreille de Vence : la première année dans la classe d’Éliane Hérinx et les deux autres dans la classe de Jean-Charles Huver.
Un changement s’impose. Petit à petit, les recherches de James se détachent de caractères figuratifs : (yeux, visages, personnages plus ou moins étranges, vaisseaux spatiaux, etc.) Il est, malgré l’investissement dans ses propres recherches, attentif et intéressé par ce que d’autres enfants produisent : il expérimente les « trouvailles » d’autres enfants en y ajoutant toujours sa touche personnelle, à savoir la recherche de symétries orthogonales. Il n’utilise plus seulement la règle ou l’équerre mais aussi le compas, compas qu’il se met aussi à employer pour vérifier l’exactitude de ses tracés. Les recherches se complexifient d’avantage.
Lors d’une présentation, un enfant dit : « Là, ce n’est plus des maths, c’est de l’art! ». Nous suivons ensemble (le groupe classe) cette piste pendant un moment : les enfants cherchent des oeuvres d’artistes qui font penser aux travaux de James. L’artiste qui a fait l’unanimité est Vasarely.
James, interrogé, explique que lui, quand il se lance dans une recherche, ne cherche pas au départ à faire quelque chose de beau mais plutôt à faire un travail compliqué sur la symétrie. Il explique aussi qu’il aime bien les « choses symétriques », l’ordre.
Quelques enfants ont aussi ramené des tableaux en fil. Ils les ont regardés mais cela n’a pas été plus loin. Ils ont continué à travailler sur des feuilles.
A la fin de la première année, James était devenu une « référence » en matière de symétrie orthogonale. Les enfants allaient le voir pour lui demander une explication, de l’aide, un avis ou même pour lui demander de préparer une symétrie à compléter. A chaque fois, James répondait positivement à toutes ces demandes. Sauf à une, celle du maître : toute la première année, de temps en temps, et sans trop insister, je lui avais proposé de travailler sur autre chose qu’une feuille quadrillée, sur une feuille blanche et il avait refusé. En y réfléchissant, ce refus était certainement lié au fait qu’il était toujours dans une phase active de recherche personnelle, d’exploration du quadrillage et de ses possibilités, de dépassement de ses propres limites. Il n’était tout simplement pas encore prêt et disponible pour les demandes du maître. James découvre le papier millimétré qu’un groupe d’enfants de dernière année du cycle 3 utilisait pour réaliser des graphiques. Pendant un moment, il l’utilisera pour réaliser ses recherches de symétries orthogonales. Il reviendra ensuite rapidement au quadrillage « simple » de ses feuilles de classeur format Seyes.
|
Une pratique, un outil : la cage à fils
 |
Revue en ligne CréAtions n° 222 "Arts et Maths" Classe CP/CE1, École Marie Curie, Lisieux (Calvados) - Enseignante : Pascale Borsi |
|
Une pratique, un outil : la cage à fils Tâtonnement autour d'un outil conçu par Paul Le Bohec Création de figures géométriques en volume
Aucune consigne ou obligation n’était associée à l’atelier cage à fils, les enfants observaient, imitaient, proposaient ou amélioraient. Sur les conseils de Paul, et pour réengager les créations vers le volume, j’ai supprimé les fils de couleurs et proposé des élastiques plus gros qui permettaient de mieux visualiser les créations obtenues. J’ai pu constater ainsi, comme pour le dessin libre au bic ou au feutre noir, qu’ une certaine « austérité » permettait de porter attention aux lignes, aux formes, d’entamer de véritables recherches originales alors que la couleur entraînait les enfants sur des pistes plus convenues. J’avais déjà fait ce constat en utilisant une pâte à modeler brune au lieu de leur fournir un choix de couleurs. Je viens de proposer les cages à des enfants plus jeunes puisque j’ai cette année une classe de GS. Il semblerait que leur cheminement soit identique et, pour l’instant je ne limite pas le nombre d’élastiques. Ils m’en ont donc demandé plus. Le foisonnement des lignes les passionne et ils multiplient les diagonales. Ce qui est intéressant car, parallèlement, sur le dessin au tableau noir et avec uniquement des craies blanches, j’assiste à des débauches d’enchevêtrements qui paraissent les enthousiasmer énormément…. « Les besoins réels et invariants des enfants ? S’exprimer, dire sous forme symbolique ses réactions au monde, ses découvertes, ses chagrins, ses peurs, ses émotions, ses expérimentations sur la langue, Ils auront toujours mille choses à dire. » Paul Le Bohec.
|
Les jardiniers de l’imaginaire
 |
Revue en ligne CréAtions n°184 "Arts et Maths" Collectif « Les jardiniers de l’imaginaire » (Drôme) |
|
Terres naturellement colorées : un matériau nomade Création d’œuvres collectives in-situ
Déroulement des ateliers
Pour le collectif : Jérôme Guerry
|
Mon arbre imaginaire
 |
Revue en ligne CréAtions n°184 "ART ET MATHS" Classe de CE1, École Eugène POTTIER, Montpellier (Hérault) - Enseignante : Claudine Vaugelade |
|
Arbres géométriques et Haïkus
C’est à ce stade que j’intervins en faisant entrer dans la classe une reproduction de « L’arbre d’amour » de Niki de Saint Phalle. Le coloriage à la manière de Nikki de Saint-Phalle renforça les effets géométriques dans le choix des couleurs et leurs interpénétrations. Une photocopie avant coloriage fut faite de tous ces arbres.
Titres et Haïkus des arbres
|
Images vertigineuses
 |
Revue en ligne CréAtions n°184 "Art et Maths" Collège K. Thoueilles, Monsempron Libos (Lot-et-Garonne) - Enseignant : Hervé Nunez |
|
Images vertigineuses
Dans les précédents numéros de CréAtions, vous avez pu déjà lire des comptes-rendus de "résidences d’artistes" au Collège de Monsempron-Libos (*). Cette pratique qui existe depuis 8 ans, fait partie d’un dispositif qui permet à tous les élèves de fréquenter la production d’artistes contemporains. Ce dispositif complète la visite systématique de tous les élèves du collège aux expositions du Château Prieural (à 10 mn. à pied depuis le collège). Si l’intérêt de se rendre à des expositions semble plus évident, l’accueil d’un artiste permet de comprendre des attitudes et les pratiques spécifiques à chaque artiste. Cet accueil, qui se renouvelle tous les ans dans l’enceinte du collège pendant une semaine, se fait sur le mode d’un contrat qui est passé avec les artistes, en ayant bien à l’esprit que ceux-ci ne viennent pas en tant que professeurs bis ou animateurs mais "en tant qu’artistes".
- L’artiste dispose d’un lieu dans le collège :
Un thème abstrait comme vecteur d'activité artistique
Une semaine avant Noël :
Des projets « libres » en classes de 3e
|