Les dossiers pédagogiques de l’Educateur n°28-29

1^er janvier 1968

Expériences d’initiation au raisonnement logique

Recueillies par Madeleine PORQUET
Inspectrice des écoles maternelles

Bibliographie

• Mathématique modernes, mathématiques vivantes – A. Revuz – (O.C.D.L.)
• Vers l’apprentissage des mathématiques – J. Bandet (Colin-Bourrelier)
• Expériences de raisonnement mathématique à l’école maternelle – M. Porquet (Dossier pédagogique n°22)

Expériences d’initiation au raisonnement logique

« Ce n’est pas assez d’avoir l’esprit juste, le principal est de l’appliquer bien. » (Descartes)

Ce deuxième dossier consacré à l’initiation au raisonnement logique à l’école maternelle fait suite, dans le temps, au premier dossier paru l’an dernier « Expériences de raisonnement mathématique ». Nous avons retenu plus particulièrement, outre des expériences dans les petites et moyennes sections, des expériences de correspondance entre deux grandes sections, celle de J. Rosmorduc à l’école de la République à Brest et celle de J. Coatanéa à Landerneau, expériences portant sur le dernier trimestre 1966. Le premier dossier traitait du même sujet mais relatait des expériences portant sur les deux premiers trimestres de la même année.

Pour mémoire, je rappelle que ces modestes ensembles d’expériences se placent dans une double perspective :

- d’une part, dans le cadre de la pédagogie Freinet axée sur l’expression et l’activité libres des enfants, sur l’intérêt général de la classe, la ligne d’intérêt général étant recherchée dans l’expression de situations vécues en profondeur par la communauté enfants-maîtresse;

- d’autre part, dans une perspective ouverte par les notions d’ensembles, de relations, de structures. Nous devons aider nos enfants, après nous être appliquées tout d’abord à les observer dans un milieu où ils peuvent faire librement de nombreuses expériences tâtonnées, à expliciter leurs démarches, à résoudre les problèmes posés par la vie de tous les jours, à découvrir et à comprendre le milieu dans lequel ils évoluent, à former leur jugement, à raisonner leurs expériences. Pour former des esprits capables de faire face à des situations constamment renouvelées (et notre monde en évolution accélérée exige de tels esprits), il nous faut accepter avec nos enfants les situations véritables où les problèmes se posent sans que l’on sache où est la solution ni même s’il y a une solution.

Mais en même temps il nous faut partir du familier et des apports enfantins et d’autre part, connaître et accepter les connaissances, le langage, les conventions que les enfants ont acquis dans le milieu de vie familial et social : « A l’école maternelle, la base des mathématiques est une réalité, une donnée physique. Ce n’est que progressivement qu’on parviendra à la notion et à l’opération mentale », écrit Madame l’Inspectrice générale Bandet dans « Vers l’apprentissage des mathématiques » (Cahier Bourrelier).

Notre ligne générale se place résolument sous l’angle du bon sens, de l’observation et de la libre démarche enfantine : pour aider l’enfant à appréhender les structures d’un monde qui se présente devant lui dans toute sa complexité, nous partons des observations des enfants dans leur milieu, des situations vivantes qu’offre la vie de la classe, mais aussi celle des correspondants. Nous analysons ces situations en les reconstruisant, non pour en extraire une étude plus ou moins systématique du nombre, mais pour aider les enfants à dégager les relations qu’elles impliquent, les notions qu’elles recouvrent.

Madame Bandet nous indique la route à suivre : « La méthode d’approche est donc celle de la connaissance expérimentale, motivée par les besoins de l’enfant et conditionnée par son milieu. »

Elle peut être exprimée par le schéma suivant :

Dès la petite section l’enfant se trouve placé dans des situations réelles de jeu : il utilise des objets, il effectue des actions, il exprime ces actions et leurs résultats par le langage usuel.

En moyenne et surtout en grande section, on prend conscience de la situation en découvrant les qualités des objets et leurs groupements et on traduit la situation et ses transformations en langage graphique et en mots propres.

Il se trouve que sur ce chemin, nous avons retrouvé naturellement la technique primitive de l’appariement (correspondance biunivoque) :

Exemple : On met la table pour fêter un anniversaire (ou pour donner le goûter aux poupées) ; les enfants apparient alors spontanément les tables, les chaises, les assiettes, les verres, les couverts.

Dans le coin des poupées: à chaque lit ses draps, ses couvertures, sa poupée. A chaque vase son bouquet.

A chaque serviette de table lavée et mise à sécher sa pince à linge, etc.

Cette démarche spontanée provoque des groupements, des comparaisons, des évaluations grosso modo, mais aussi l’emploi d’un langage recouvrant, de façon fort imprécise mais qui constitue une approche, des notions mathématiques: pareil, autant que, plus que, moins que, beaucoup, peu, etc.

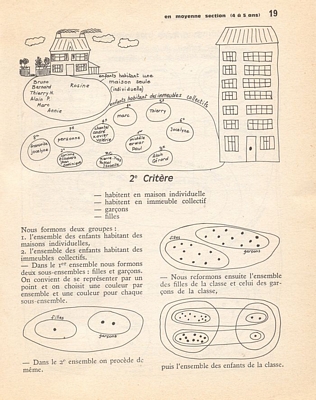
Mais la diversité du matériel nous oblige à ordonner notre univers, à opérer des classements :

- classements agis,
- puis réflexion sur ces classements qui provoque la constitution d’ensembles,
- puis recherche d’autres critères de classement et constitution de nouveaux ensembles. Ainsi à partir de remarques sur leurs vêtements, sur les objets de déguisements, on arrive à des classements divers:
- dans le coin cuisine, on peut rechercher et grouper ce qui sert à la préparation des repas, ce qui constitue le repas lui-même, ce qui sert à mettre la table, etc.
- dans le coin jouets, on peut classer les autos; par ex.: suivant leurs formes puis leurs usages,
- dans la boutique: on classe les emballages suivant différents critères

a) les qualités du contenu: ce qui se mange, ce qui se boit, ce qui ne se mange ni ne se boit,
b) les qualités du contenant: ce qui est en paquets, en flacons, en pots de carton, de plastique, etc.
c) la nature des objets: huile, allumettes, fromages, etc.

Ce grand ensemble des objets qui se vendent peut être décomposé de différentes façons: il contient toujours les mêmes objets: cette notion de conservation de la quantité, si difficile à acquérir, sera lentement perçues à travers ces multiples classements et tris effectués librement par les enfants dans tous les coins de jeux puis exprimés. Nous pouvons susciter des classements en vivant avec les petits groupes de jeu les situations agies, mais nous pouvons aussi susciter des classements individuels.

Voici, dans cette perspective, des expériences menées dans la classe de Micheline Barré à Rouen.

en petite section (de 3 à 4 ans)

Les ensembles
à partir des découpage libres des enfants

Dans une classe très chargée (50 enfants), un excellent travail libre individuel a pu être réalisé à partir du découpage des catalogues.

Les enfants découpent librement des catalogues puis ils collent les figurines découpées sur une grande feuille en les groupant spontanément. Outre l’apprentissage naturel de la technique du découpage, ils acquièrent peu à peu la notion de groupement des objets selon un critère qu’ils découvrent a posteriori. Il s’agit là véritablement du tâtonnement expérimental à l’état brut.

L’enfant découpe et colle d’abord sans aucune idée de groupement. Deux exemples:

- des savonnettes, un divan, un paysage,
- un soldat, une coupe de fruits, un paysage.

Puis en « racontant » les collages, les enfants perçoivent les rapports des objets entre eux. Exemple :

- dans une page, il y avait plusieurs chaussettes, un chausson et une cuvette avec un broc. Les enfants, après discussion entre eux; ont décollé la cuvette et le broc; «Ça ne va pas avec». Sur une autre page comportant serviettes de toilette, ils ont retiré un lit et une housse-penderie. Mais ces éléments retirés n’ont pas été perdus. Le lit est allé sur une autre feuille des couvertures, des draps, taies, traversins et oreillers qu’une fillette avait déjà collés.

Enfin, à la suite de ces discussions de ces rectifications nées de la critique mutuelle, les enfants en arrivent rechercher des objets présentant en eux des rapports précis et à les col en fonction de ces rapports.

Ainsi, du collage confus, se dégagent peu à peu des ensembles précis caractères bien définis. Ex. :

- des mamans qui vont se promener (silhouettes de femmes en manteau vestes et jupes, anoraks et pantalon
- des mamans qui travaillent tablier ou devant des machines laver).

D’un ensemble peuvent se dégagent deux sous-ensembles. Ex. :

- dans l’ensemble des papas, on cernera le sous-ensemble des papas ayant un chapeau et le sous-ensemble des papas sans chapeau,
- dans un collage de bébés-jouets, ils distingueront le sous-ensemble des baigneurs et celui des poupées,
- le sous-ensemble des objets nécessaires à la coiffure (bigoudis, épingles, casque-séchoir, brosse, peigne) est dégagé de l’ensemble des objets de toilette (cuvette, savonnette, éponge),
- dans un ensemble de jouets, les enfants distinguent spontanément ce qui roule et ce qui ne roule pas : « Ces voitures-là, elles ne roulent pas, elles sont dans les boîtes en plastique ». Grosse discussion car les roues n’impliquaient pas que ça puisse rouler, c’est logique,
- le sous-ensemble des jouets à trois roues est isolé dans l’ensemble des jouets à roues (vélos, tricycles, autos, landaus).

Parfois l’enfant essaie de réaliser un ensemble d’objets différents autour d’un thème comme le lit avec ses accessoires. Par exemple :

- Serge groupe sur une feuille un lit avec un dessus de lit à fleurs semblable au sien, une maman accrochant des rideaux, une armoire, une coiffeuse, une fillette en combinaison et deux garçons en pyjama. Puis il commente
« J’ai fait ma chambre avec ma maman, moi, mon frère, ma sœur. »

Cette confrontation continuelle amène l’enfant à découvrir la correspondance terme à terme. Ex :

Florence a collé des petites voitures. Serge lui demande :

- C’est à qui ces autos-là ?
- A des petits enfants.
- Ils sont partis, les petits enfants ?
- Non, je vais les découper.

et elle colle un enfant sous chaque voiture. Annick a collé des papas et des chemises, mais en les rejoignant par un trait, elle s’aperçoit qu’un papa n’a pas de chemise. Vite, il faut intercaler celle qui manque.

Isabelle a remarqué que sur deux panoplies de moules en plastique découpées dans le catalogue « C’est pareil ! »"

- Comment pareil ? (en effet les moules sont tous différents).
- Oui regardez.

Et elle commence à joindre deux à deux les moules de chaque panoplie. A la fin la maîtresse doit aider un peu à ne pas mélanger les traits.

Conclusion : Isabelle a perçu spontanément que dans les deux panoplies il y avait le même nombre de moules (24 dans chaque).

Corinne a collé des papas puis une botte sous chaque papa jusqu’au moment où Christophe lui a dit : « Le papa, il ne peut pas marcher avec une botte, il a deux pieds ! »

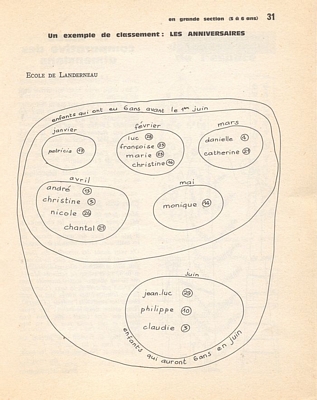
Le calendrier

L’ensemble des jours du mois est perçu sous des formes différentes :

a) le calendrier est affiché sous la forme d’une bande de 50 cm de haut, tout autour de la classe. Une couleur différente pour chaque semaine, chaque jour a une case de 50 X 30 cm où l’on colle un dessin,

b) sur la porte, un calendrier plus petit (70 X 50 cm) pour le mois. Les semaines sont de la même couleur que sur le grand calendrier. On y dessine chaque jour le temps qu’il fait (soleil, pluie, brouillard, vent). Les jours de congé sont marqués d’une croix,

c) le calendrier commercial du mois encore plus petit et présenté différemment où l’on repère le jour par la couleur correspondante.

Les comparaisons entre les présentations différentes du temps écoulé sont multiples, à l’intérieur de chaque mois, par semaine, puis les enfants en arrivent à composer deux ou plusieurs en-ensembles-mois.

L’anniversaire n’est plus seulement un bon souvenir ; Yvon sait qu’il a eu 4 ans dans le mois où il y a « beaucoup de croix », il sait aussi que Pascale a eu ses 4 ans dans le mois « où il fait tout gris » et que Jean-Paul a soufflé ses bougies un jour de soleil. Au travers de ces multiples liens affectifs, les enfants structurent leur notion du temps. Leurs activités les mettent dans des situations où la réflexion n’a guère de répit ; le coin cuisine où l’on aime tant se retrouver avec le vrai matériel et le réchaud électrique est lui aussi l’occasion de comparaisons, d’estimations et contribue au raisonnement mathématique.

EXPÉRIENCES DE RAISONNEMENT CHEZ LES GRANDS

Nous avons vu dans le précédent dossier :

1. Prise de conscience du temps : le calendrier.
2. Prise de conscience de l’espace-classe et du groupe enfants : découverte de sa pace au sein du groupe et au sein de l’espace-classe et repérage sur un plan qu’on construit soi-même.
3. Prise de conscience de l’espace-école : plan de l’école.
4. Sens de la direction : le vent.
5. Les tailles des enfants
6. Les pointures
7. Les pesées.
8. Les ensembles spontanés : dans ma ferme.
(études comparatives des dimensions)
9 et 10. Classements divers des enfants, frères et sœurs, vêtements des jambes.
11 et 12. Classements des éléments d’un ensemble : le bouquet, le calendrier d’octobre,

Voici à titre indicatif, quelques classements réalisés dans différentes classes de grand :

- véhicules à moteur ou sans moteur
- véhicules ayant 1 ou 2 ou 3 ou 4 ou beaucoup de roues
- bateaux à voile, moteur, rames
- mémés avec ou sans coiffe
 - jours avec ou sans école.

Avant la présentation des expériences de correspondance entre deux grandes sections, voici des notes concernant des travaux réalisés dans la classe de Monique Delbasty et exposés au congrès de Tours ainsi que quelques documents sur les partages et l’atelier de calcul.

a)Plans et itinéraires :
- le chemin pour aller à l’école,
- les routes du village,
- graphe du trajet aller et retour quatre fois par jour de la maison à l’école.

b) Relations entre les ensembles :
découverte des relations : « a pour correspondant »
« donne la main à »
« a une voiture »
« a pour lit : les enfants qui couchent seuls ou non seuls »
et schématisation de la relation entre les ensembles :
Ex.: relation « a pour correspondant » bijection : chacun des enfants de la classe a un correspondant dans l’autre classe.
Ex. : relation « a pour lit »
surjection : Jean et Paul couchent dans le même lit
Marie couche seul
Jeanine couche seule
Pascal et Thierry couchent dans le même lit.

c) les permutations : à table j’ai changé de place avec Yves.

d) schématisation des tailles comparées des membres de chaque famille (notions de grandeur et d’ordre).

e) Géométrie :: notion de symétrie (visage, corps, dessin)
- établir la correspondance entre les différents points de deux dessins semblables mais de tailles différentes.

f) Mesure du temps :
- ceux qui sont allés se coucher tôt
- ceux qui ont entendu une émission particulière de radio, de télévision.

g) Graphes des mouvements

Les partages

Les crêpes du Mardi-Gras

Mardi 7 février:
La maîtresse a apporté trois douzaines de crêpes, par paquets de 6.
Les enfants défont les papiers.
Claudie : II y a 6 paquets.
La maîtresse sépare les crêpes, les enfants regardent les crêpes étalées sur la table.
Gilles : Il y a 6 crêpes dans un paquet.
Pascal K.: Oui, 3 et 3 ça fait bien 6.
Maîtresse : Combien y a-t-il de crêpes en tout maintenant ? Comment faire pour trouve ?
Gilles : On va faire des crêpes en papier.
Les enfants prennent du papier d’emballage, se groupent. Ils découpent 6 crêpes et font un paquet. Puis 6 autres crêpes et font un deuxième paquet... Ils découpent ainsi 6 paquets de 6 crêpes.
Ils comptent (3 enfants : Claudie, Gilles et Thierry ont trouvé 36 crêpes).
Thierry: J’ai dit 6 et 6, 12, et puis après 12 et 2, 14, puis 14 et 2, 16... jusqu’à 36.
Claudie et Gilles ont dit 6 et 6, 12, puis ils ont ajouté une crêpe ensuite.
Michel: On pourra jamais les partager dans notre tête !
Claudie: On pourrait en donner une à chacun et on verra bien s’il en reste.
Michel prend les crêpes et décide d’en donner deux à chacun parce qu’il y en a beaucoup, dit-il (il y a 20 enfants présents).
Il distribue deux crêpes à chacun, mais deux enfants n’en ont pas.
Michel: Il faut en donner une seulement à chacun.
Cette fois il en reste beaucoup.
Xavier : Si on en avait donné 3, il n’en resterait pas!
Gilles : Mais non, avec 2 chacun, il n’y en avait pas assez!
Michel : Moi, je ne sais pas comment partager le reste!
Françoise: Je vais couper celles qui restent en 2, puisqu’il n’y en a pas assez pour que tout le monde en ait une autre, on verra bien si ça va!
Elle coupe les crêpes restantes et distribue une moitié à chaque enfant.

Classe de Mlle JACOB – École LAENNEC - BREST

A l’atelier de calcul

Mercredi 25.1.67

Bruno se plaît aux balances (Roberval ; il a déjà équilibré ses plateaux avec divers récipients contenant du sable. Aujourd’hui il a rempli une tasse d’eau et il assure l’équilibre en versant du sable dans une tasse sur le 2e plateau de la balance. I1 est heureux, la flèche est juste- au milieu, il ne veut plus y toucher.

Vendredi 27.1

Bruno s’aperçoit que le plateau de la balance penche du côté sable. Il se fâche et dit :
- Quelqu’un a chaviré un peu d’eau!
 - Voyons, personne n’est venu ici hier.
 - «Plume» (la tourterelle) est peut-être venue boire alors.
- La cage était fermée, ce n’est pas possible.

Il réfléchit, mais ne trouve pas.

Maîtresse: N’as-tu jamais regardé des flaques d’eau dans la cour?
Bruno: Je sais, l’eau a séché un peu: Il rétablit l’équilibre : II ne faut que deux bigorneaux aujourd’hui.

Lundi 30.1

Bruno : L’eau a séché beaucoup aujourd’hui  j’ai mis cinq bigorneaux pour mettre l’aiguille au milieu.
Alain: Parce que c’était dimanche hier.
Bruno: Oui, elle a séché pendant deux jours.

La maîtresse pose la balance sur une table à proximité du radiateur et en plein soleil. D’autre part elle place un couvercle de boîte rempli d’eau sur le radiateur.

Le soir on constate qu’il n’y a plus d’eau dans le couvercle qui est complètement sec; aux balances, le plateau côté «sable» penche de nouveau. Bruno, d’une légère pression des doigts, apprécie ce qui manque pour rétablir l’équilibre, et essaie d’ajouter de plus gros coquillages. L’aiguille n’est pas juste au milieu, il a l’idée d’enlever un bigorneau tout petit qu’il met sur le plateau côté «sable».

- Ça y est! Il est parti beaucoup d’eau cette fois-ci!
- Pourquoi?
Alain: Elle sèche plus vite quand i1 fait chaud.
Jocelyne: On n’a pas vu l’eau partir de la boîte.
Maîtresse: Je suis sûre que vous avez vu l’eau partir quelquefois!
Jacques: Oui, quand maman ouvre la cocotte-minute, ça fait de la vapeur, alors maman la met sur la fenêtre parce que c’est de l’eau qui part.
Thierry: L’eau de la tasse est partie par la fenêtre dans le ciel.

La correspondance entre les deux grandes sections de Brest République (J. Rosmorduc) et Lanterneau M. Curie a permis d’aborder l’an dernier le programme suivant (échanges des documents et comparaisons entre les deux classes)

1. Classements et relations :
- les écoles: classes et enfants (p. 30)
- les dames de chacune des écoles
- les familles des enfants de chacune des deux classes
- les voitures
- les animaux
- les véhicules
- le temps du mois de mai
- les anniversaires (p. 31)

2. Étude comparative des dimensions (p. 32): (tailles, pointures, sapins de Noël, lentilles, fèves, jacinthes).

3. Prise de conscience de l’espace environnant: plans de la classe, de l’école, des jardins (P- 33), des maisons, du quartier, itinéraires.

4. Les formes géométriques: le cercle (p. 34), le carré, triangle, rectangle, ovale (points de départ : les napperons, les jardins publics).

5. Prise de conscience des forces créatrices de mouvements:

 - Notion d’équilibre : le fil à plomb (p. 35)
- déplacements: jeu des cordes (p. 36), jeu du cheval, la brouette
- construction de mobiles
- le moulin à vent (p. 37)

6. Prise de conscience des mouvements:

- Sens
- vitesse: le chemin de l’école (p. 38), les avions (p. 38), les fusées (p. 39), les accidents (p. 40)
- comparaisons de mouvements en sens et vitesse: train et voiture (p. 41)
- transformations dues au mouvement: train et wagons (p. 45)
- les permutations.

7. Prise de conscience du temps: le calendrier, l’heure (p. 46).

8. Notion de partage: le poisson (p. 46)

9. Les rapports: étude comparative de deux oiseaux: hibou et tourterelle

- rapport volume-poids
- rapport poids-longueur des ailes
- rapport taille-rapidité du vol (p. 47).

10. Les sons :

- 1a sirène
- le train
- les tourterelles
- le tambourin

tracés intuitifs de courbes traduisant la variation de l’intensité d’un son dans le temps (p. 48)

11.. L’usine (p. 48).

II. Étude comparative des dimensions

LE SAPIN DE NOËL

Chers amis, notre sapin est arrivé dans un camion.
II est grand! Plus grand que la maîtresse! Pour le mesurer, la chaise n’était pas assez haute. On a pris l’escabeau. Madame Le Roy a tenu le sapin. Madame Rosmorduc a tenu la bande de papier tout en haut et Éric l’a coupée en bas.
Madame Coatanéa devra monter tout en haut de l’escabeau.

Brest République

Chers amis de Lanterneau,
Merci pour les crêpes, c’était bon. Merci pour les masques, les chapeaux et les confetti: on s’est bien amusé. On en a jeté sur ceux des autres classes, sur les maîtresses, sur les mamans à 5 heures!
On vous donne des nouvelles des fèves: elles sont hautes, hautes, elles ne tiennent plus, elles se couchent, elles ont des feuilles: 4, 6, 8, 12 et même 14 (celle de Marc), on va les planter toutes ensemble dans un grand pot avec de la terre (Corinne). Et vos lentilles? Les nôtres font un petit champ tout rond dans l’assiette (Thierry). Nous avions deux jacinthes: une grosse bleue qui s’est cassée: elle était trop lourde et une petite rose qui va bien (Christine).
On a joué au football: les garçons ont gagné 7 buts et les filles 5.
Christian et Philippe étaient les goals.
Au revoir!

Brest République

III. Prise de conscience de l’espace

Chers amis de Lanterneau,
Elles sont belles vos maisons; nous allons bientôt vous envoyer les nôtres, nous n’avons pas beaucoup de jardins, seulement des cours.
Ceux qui ont un jardin: André, Jean-Luc, Daniel (il nous apporte des camélias blancs de temps en temps) Philippe Kerriou, Xavier.
Nous habitons presque tous dans de grandes maisons, pas des HLM, des immeubles!
On a dessiné des jardins: d’abord des rectangles et puis des carrés et des ronds (celui de la place Sanquer) et puis des pointus; c’est Gilles qui a su les trouver et dire le nom: triangle. Essayez de faire un carré avec les enfants, c’est difficile! Un rond, c’est facile, un rectangle aussi, même un triangle, mais pour le carré on a eu du mal.

Réponse de Landerneau

Chantal: J’ai une idée pour le carré. Je prends quatre enfants de la même hauteur et je les allonge, ça fait un carré.
Christian: j’ai une autre idée, je prends 2 enfants puis 2, puis 2 et 2 encore et je fais 4 côtés
Danielle: Une autre idée : assis par 4.
Mêmes idées pour le rectangle et le triangle.
Représentation: Comment faire un vrai carré sur la feuille?
Christian: Je coupe 4 bandes de papier pareilles et je colle.
Avec une ficelle, je fais des marques. Thierry
 Avec un bout de bois, je trace 4 traits pareils. Jacques.

IV. Les formes géométriques

Découverte du cercle comme lieu géographique des points équidistants du centre

ÉCOLE DE LA RÉPUBLIQUE A BREST

Comment avons-nous fait le cercle? Dans la cantine, on forme une ronde et on regarde.
Christine: Ça n’est pas bien rond. Maîtresse, mets-toi au milieu.
Maîtresse: Où dois-je me mettre?
Christine place la maîtresse approximativement au centre de la ronde.
Maîtresse: Est-ce bien? Suis-je juste au milieu?
Éric: Pour le savoir, il faut mesurer: i1 faut que ce soit 1a même chose entre Daniel et toi qu’entre toi et Philippe.
Jean-Luc: Pour mesurer on peut prendre une ficelle.
Il essaie mais a beaucoup de mal à maintenir la ficelle tendue.
Christine: Avec le bâton du tableau ça ira mieux.
Elle va chercher le bâton, en place une des extrémités aux pieds de Daniel puis place la maîtresse à l’autre extrémité.
Ensuite elle retire le bâton, en place une extrémité aux pieds de la maîtresse et place Philippe à l’autre extrémité.
Maîtresse: Très bien, et maintenant, suis-je bien au milieu de la ronde?
Christine: Il faut faire la même chose pour tous les enfants.
Elle déplace le bâton successivement des pieds de la maîtresse vers chacun des enfants, place chacun à l’autre extrémité et trace à la craie les rayons du cercle.
On rentre en classe et chacun trace sur un papier, au moyen d’un bâton, pour son correspondant, la figure ainsi  obtenue.
Gérard: Mon frère fait la même chose avec son compas.

Chers petits amis de Landerneau

On s’est bien amusé avec les cercles. Ici Christine B. a pris une baguette: la grande qui sert à montrer les textes, pour mesurer entre la maîtresse et les enfants et elle a dessiné à la craie sur le plancher tous les rayons: ça faisait un grand soleil.

Pour vous dessiner les cercles, nous avons pris des petits bâtons: d’abord, ça faisait un arbre, et puis un éventail et puis un parapluie, une étoile et puis une roue de bicyclette.

CHEZ LES CORRESPONDANTS

La démarche est à peu près identique, mais le bâton du tableau s’étant révélé «trop petit», on utilise une ficelle: André et Christine sont dans la ronde de part et d’autre de la maîtresse placée approximativement au milieu.

Catherine: 11 faut que ce soit pareil du côté d’André et du côté de Christine, on va leur faire une marque.
Maîtresse: Et après?
Philippe: On fait pareil pour et Luc.
Tous les enfants ayant été placés, on passe au travail individuel.
Représentation: Comment va-t-on faire un vrai rond sur la feuille?
Jean-Luc: On pose le papier sur une assiette et on coupe.
Chantal: On marque les places avec un morceau de bois.
Mais nous n’en avons pas.
Danielle: Avec un bout de ficelle.
Nous avons de la laine.
Chacun vient couper un morceau de laine et construit son cercle.
Ainsi, la définition du cercle en tant que lieu géométrique des points équidistants du centre a été découverte.

V. Les forces

ÉCOLE DE LANDERNEAU

Philippe D. a fabriqué à l’atelier de bricolage "un jeu»: une ficelle au bout de laquelle il a fixé un morceau de bois.

- Qu’as-tu fait?
- C’est pour voir si le bois est lourd.

Chacun veut essayer.
- Oui, on sent (Thierry).
- On sent que le bois est lourd (Philippe).
- Ça tire sur le bras (Nancy).
- Vers le bas (Catherine).
- Si on tâche la ficelle, ça tombe (Jacques).
- La ficelle est droite (Philippe).
- Si on lâche la ficelle, ça fait comme un serpent parce que c’est mou (Thierry). - Ça va toujours vers le bas (Chantal).

Représentation

- Comment peut-on montrer que le bois tire vers le bas?
- On peut mettre une flèche (Philippe).

Jeu des cordes

Christian et Hervé se disputent une corde et tirent à qui mieux mieux.
Éric: C’est Hervé qui a gagné: c’est lui le plus fort.
Nous organisons ce nouveau jeu: une corde pour deux.
Philippe: Comme ça on pourra savoir qui a le plus de force.
Après le jeu:
- J’ai gagné, j’ai plus de force que Joël (Hervé).
- J’ai perdu, je suis la moins forte (Catherine).
- Mais pour Thierry et Jacques, on ne sait pas (Alain).
- Si Thierry «aurait» été plus fort, ça aurait été tout par là (geste du bras) (Catherine).
(Maîtresse) - Qui a gagné alors?
- Tous les deux (Chantal).
- Qui a perdu? (Maîtresse)
- Aucun, ils sont farts tous les deux (Marc),
- Ils sont pareils (Chantal).
- Ils ont une farce pareille (Catherine).
- Comment dit-on encore ? (Maîtresse)
- ils sont en équilibre (Philippe)
- Ils ont la même force (Christian)
- On dit aussi une force égale (Maîtresse)
Représentation
Introduction des signes     = >     <
Force de Thierry -= force de Jacque
Force de Philippe <                    force de Marc
Je suis plus fort que Philippe. Ça va par là ->.(Marc)
- Philippe ne devrait pas avoir flèche alors puisque tout va par là. (Thierry).
- Philippe ne tirait pas du tout?
- Si mais un peu seulement.
- Alors on peut lui mettre une plus petite flèche parce qu’il n’est pas si fort.

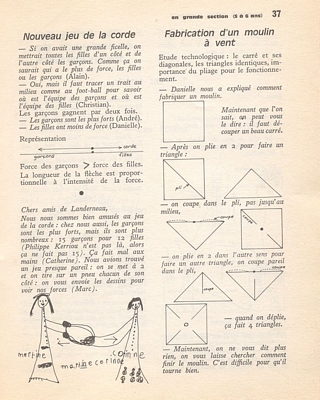
Nouveau jeu de la corde

- Si on avait une grande ficelle, on .mettrait toutes les filles d’un côté et de l’autre côté les garçons. Comme ça on saurait qui a 1e plus de force, les filles ou les garçons (Alain).
- Oui, mais il faut tracer un trait au milieu comme au football pour savoir où est l’équipe des garçons et où est l’équipe des filles (Christian).
Les garçons gagnent par deux fois.
- Les garçons sont les plus forts (André).
- Les filles ont moins de force (Danielle).
Représentation
Force des garçons > force des filles.
La longueur de la flèche est proportionnelle à l’intensité de la force.

Chers amis de Landerneau,

Nous nous sommes bien amusés au jeu de la corde: chez nous aussi, les garçons sont les plus forts, mais ils sont plus nombreux: 15 garçons pour 12 filles (Philippe Kerriou n’est pas 1à, alors ça ne fait pas 15). Ça fait mal aux mains (Catherine). Nous avions trouvé un jeu presque pareil: on se met à 2 et on tire sur un pneu chacun de son côté ; on vous envoie les dessins pour voir nos forces (Marc).

Fabrication d’un moulin à vent

Étude technologique: le carré et ses diagonales, les triangles identiques, importance du pliage pour le fonctionnement.
- Danielle nous a expliqué comment fabriquer un moulin.
Maintenant que l’on sait, on peut vous le dire : il faut dé­couper un beau carré.
- Après on plie en 2 pour faire un triangle :
- on coupe dans le pli, pas jusqu’au milieu,
- on plie en 2 dans l’autre sens pour faire un autre triangle, on coupe pareil dans le pli,
- quand on déplie, ça fait4 triangles.
- Maintenant, on ne vous dit plus rien, on vous laisse chercher comment finir le moulin. C’est difficile pour qu’il tourne bien.

VI. Prise de conscience des mouvements

1. Les trajets

Brest

Chantal pour son correspondant:
- Le matin je vais tout droit de ma maison à l’école.
- Le midi je pars de l’école, je vais au lycée chercher mon frère et je rentre à la maison.

Landerneau, 23 janvier

Hervé raconte qu’il est allé à Bodélis sur le terrain d’aviation :
- J’ai vu un avion décoller, ça fait du bruit, il faut se boucher les oreilles, ça fait du vent, on ne peut plus courir.
- Dessine-nous l’avion que tu as vu.
 Philippe: Moi, j’aimerais bien aller en avion. L’avion roule sur la piste puis après il décolle, il monte comme ça (geste) et il rentre ses roues.
- Viens dessiner l’avion qui décolle.
 Éric: Quand il est dans le ciel, je sais comment il est (nouveau dessin).
Hervé: Et quand il descend, il fait ça.
Yann: On peut mettre les flèches pour dire où il va.

A l’atelier de bricolage, Éric construit un avion et le lendemain nous montre comment l’avion roule sur la piste, décolle, tourne, monte, descend, atterrit.
Plusieurs enfants viennent faire le même jeu.
Représentation : Chacun représente un avion et doit le conduire où il veut mais doit savoir par des flèches indiquer le trajet de son avion.

Claudie envoie aux correspondants la page ci-contre:

Chers amis de Brest,
Devinez ce que je vous ai dessiné.

Réponse de Brest

Chère Claudie, on a deviné: l’hélicoptère roule, puis décolle et rentre ses roues, puis il monte, puis il redescend, puis il roule.

2. - Les fusées

24 janvier, Landerneau
Éric: Moi, j’aimerais bien aller dans une fusée. Après on irait dans l’espace.
Jean-Luc: Oui, mais ça fait peur.
André: Non, la fusée monte, monte comme ça, après elle devient toute petite quand elle est en haut.
Philippe: Ça va chatouiller le ventre alors.
Chantal: Si 1a fusée va dans les nuages, on verrait notre maison toute petite.
Thierry: Après la fusée, elle tournerait autour de la lune, ou de la terre, je n’sais pas trop. Je n’sais pas non plus quelle hauteur a le ciel.
Claudie: Quand on monte dans le ciel et quand on tourne autour de la lune, ça doit être drôle, c’est facile à faire une fusée.
La représentation ci-contre est envoyée aux correspondants sans explications.
- Devinez.
Après quelques suppositions erronées (C’est une maison avec un bonhomme; c’est un soleil), on trouve la réponse.
-  C’est une fusée qui monte et qui tourne autour de la lune.

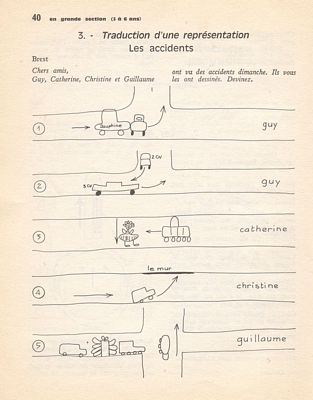
3. Traduction d’une représentation

Les accidents

Brest

Chers amis,

Guy, Catherine, Christine et guillaume ont vu des accidents dimanche. Il vous les ont dessinés. Devinez.

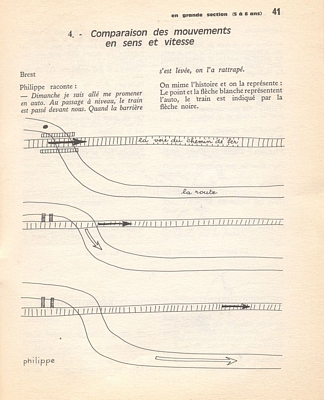
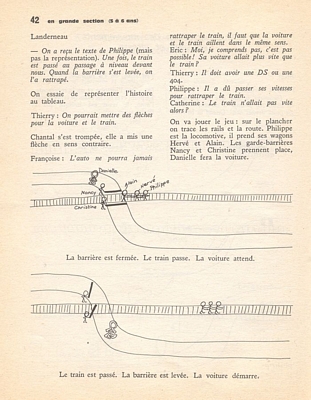
4. - Comparaison des mouvements en sens et vitesse

Brest

Philippe raconte:

- Dimanche je suis allé me promener en auto. Au passage à niveau, le train est passé devant nous. Quand la barrière s’est levée, on l’a rattrapé.

On mime l’histoire et on la représente: Le point et la flèche blanche représentent l’auto, le train est indiqué par la flèche noire.

Landerneau

- On a reçu le texte de Philippe (mais pas la représentation). Une fois, le train est passé au passage à niveau devant nous. Quand la barrière s’est levée, on l’a rattrapé.

On essaie de représenter l’histoire au tableau.

Thierry: On pourrait mettre des flèches pour la voiture et le train.

Chantal s’est trompée, elle a mis une flèche en sens contraire.

Françoise: L’auto ne pourra jamais rattraper le train, il faut que la voiture et le train aillent dans le même sens.

 Éric: Moi, je comprends pas, c’est pas possible! Sa voiture allait plus vite que le train?

Thierry. Il doit avoir une DS ou une 404­

Philippe: Il a dû passer ses vitesses pour rattraper le train.

Catherine: Le train n’allait pas vite alors ?

On va jouer le jeu: sur le plancher on trace les rails et la route. Philippe est la locomotive, il prend ses wagons Hervé et Alain. Les gardes-barrières Nancy et Christine prennent place, Danielle fera la voiture.

La barrière est fermée. Le train passe. La voiture attend.

Le train est passé. La barrière est levée. La voiture démarre:

La voiture a passé ses vitesses et rattrapé le train.

Le lendemain on dessine rails et route pour les correspondants, on construit un train, Yann apporte une voiture, nous jouons à les faire circuler sur le trajet.

Représentation individuelle:

Chaque enfant refait le circuit dans les 3 positions et suivant l’idée de Thierry y place des «flèches-vitesse.»

Marc: La voiture rattrape le train, elle va plus vite que lui.
Danielle: Alors il faut lui mettre une grande flèche.
Nancy: Pourtant la voiture va moins vite au début.
Alain: Ben, on lui mettra une petite flèche au début.
Catherine: Et quand la barrière est fermée, la voiture est arrêtée. Alors on ne lui met pas de flèche.

Landerneau

On a beaucoup de choses à vous demander:
- Moi je voudrais savoir quelle voiture a Guillaume?
- Ça doit être une 404 ou une DS, ça va plus vite parce que c’est plus lourd (Thierry).
- C’est plutôt une Mercédès parce que ça va encore plus vite (Hervé).
- Qui conduisait la voiture? (Chantal).
- Il a dû passer ses vitesses pour rattraper le train (Philippe).
- C’était une locomotive à vapeur ou une Diesel ? (Éric).

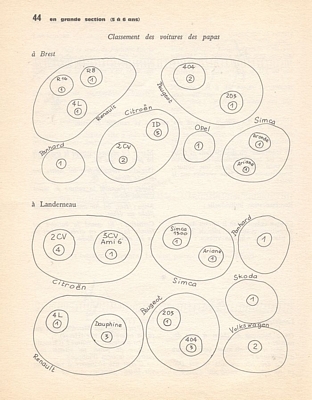
Classement des voitures des papas

À Brest

À Landerneau

Transformations dues au mouvement

Chers amis de Landerneau,

Ça c’est le chemin de la locomotive que nous avons vue hier à la gare: elle est partie du gros point avec 5 wagons. Elle les a laissés au garage, elle a changé de rails sur un aiguillage, et puis elle a reculé pour aller hercher d’autres wagons, elle a encore^’ changé de rails; elle est repartie en avant avec 5 autres wagons.

Nous sommes restés à la regarder longtemps : elle recommençait toujours la même chose.

C’est nous sur la passerelle de la gare. Christine a dessiné les filles, Gilles les garçons.

VII. Prise de conscience du temps - L’heure

Chers amis
Éric nous a dit:
- Le matin, je sais à quelle heure je me lève et je déjeune.
- Philippe M., Thierry, Danielle et beaucoup d’autres ont dit qu’ils se levaient à la même heure.
- On vous laisse deviner à quelle heure on se lève.
- Et vous est-ce la même heure ?
- je sais aussi à quelle heure je pars à l’école (Éric).
- Et, est-ce que c’est pareil pour vous?
- Et quand l’école commence il est..... mais on ne vous dit rien. Cherchez.
- Et vous, à quelle heure commence votre école ? On voudrait savoir si c’est comme chez nous.

VIII. Notion de partage - Le poisson

Chers amis de Brest,

A Concarneau mon pépé a acheté un gros, gros lieu. Après il l’a mis sur une grande pierre et avec son couteau i1 a coupé la tête et puis la queue. Avec la tête, mémé a fait de la soupe et pépé a donné la queue au chat. Après il a coupé le lieu en 4. d’abord et en 3 après.

On vous demande:

- combien de morceaux de poissons y a-t-il ?
- combien de "coups de couteau» le pépé de Christian a-t-il donné pour couper le poisson
- pour manger le lieu il y avait: le papa, la maman, le pépé, la mamie et Christian. Est-ce qu’il y avait assez de morceaux?
Combien en trop?
Cherchez.

IX. Les rapports

Étude comparative de 2 oiseaux : HIBOU ET TOURTERELLE
longueur des ailes, rapport taille-rapidité du vol

Chers amis de Brest,

Le hibou de Philippe a des grandes ailes, plus grandes que celles des tourterelles. On peut les mesurer (Thierry).

«Petite Neige» (une tourterelle) a des plus grandes ailes que "Cléo» (l’autre tourterelle) mais plus petites que celles du hibou (Catherine).

- Alors le hibou vole plus vite que les tourterelles ? (Philippe)

- Oui, parce qu’il a des plus grandes ailes (Éric).

- Alors, Cléo vole moins vite que Petite-Neige? (Danielle)

- Non, ils volent à la même vitesse, parce que ce sont des tourterelles toutes les deux (Christian).

- Moi je crois que Philippe a raison, parce que moi je cours moins vite que ma soeur, parce que je suis plus petit (Marc).

- Oui et puis un petit vélo va moins vite qu’un grand parce que les roues sont moins grandes (Chantal).

- Oui, mais le hibou est gros et lourd (Éric L.).

- Oui, il est plus gros que Cléo et que Petite-Neige (André).

- Pour savoir, il faut peser (Philippe).

- Il y a des poids en plus pour le hibou : il est plus lourd (Nancy).

- II y a des poids pareils (Alain).

- Et il y en a qui ne sont pas pareils (Éric).

- Les ailes non plus ne sont pas pareilles (Thierry).

- Si on met les bandes l’une sur l’autre, on voit que celle de Cléo est juste à la moitié (Philippe).

- Non, c’est pas la moitié, c’est un peu plus (Christian).

- Les ailes du hibou sont a fois plus grandes presque et il est beaucoup plus lourd (Thierry).

- Alors Cléo doit voler plus vite (André).

- C’est difficile à savoir parce que Cléo ne vole pas la nuit (Éric).

- Peut-être que les correspondants savent mieux que nous (Nancy).

- On devrait leur demander (Alain).

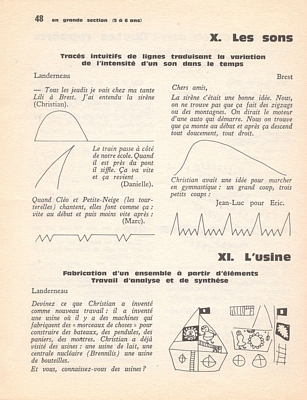
X. Les sons

Tracés intuitifs de lignes traduisant la variation de l’intensité d’un son dans le temps

Landerneau

- Tous les jeudis je vais chez ma tante Lili à Brest. J’ai entendu la sirène (Christian).

Le train passe à côté de notre école. Quand il est près du pont il siffle. Ça va vite et ça revient (Danielle).

Quand Cléo et Petite-Neige (les tourterelles) chantent, elles font comme ça: vite au début et puis moins vite après : (Marc).

Brest

Chers amis,

La sirène c’était une bonne idée. Nous, on ne trouve pas que ça fait des zigzags ou des montagnes. On dirait le moteur d’une auto qui démarre. Nous on trouve que ça monte au début et après ça descend tout doucement, tout droit.

Christian avait une idée pour marcher en gymnastique: un grand coup, trois petits coups:

Jean-Luc pour Éric.

XI. L’usine

Fabrication d’un ensemble à partir d’éléments Travail d’analyse et de synthèse

Landerneau

Devinez ce que Christian a inventé comme nouveau travail: il a inventé une usine où il y a des machines qui fabriquent des «morceaux de choses» pour construire des bateaux, des pendules, des paniers, des montres. Christian a déjà visité des usines: une usine de lait, une centrale nucléaire (Brennilis) une usine de bouteilles.

Et vous, connaissez-vous des usines?

POSTFACE

Je voudrais simplement attirer votre attention sur une définition de l’ordre donnée par Michel Foucault dans Mes mots et les choses :

« L’ordre c’est à la fois ce qui se donne dans les choses comme leur loi intérieure, le réseau secret selon lequel elles se regardent en quelque sorte les unes les autres, et ce qui n’existe qu’à travers la grille d’un regard, d’une attention, d’un langage, et c’est seulement dans les cases blanches de ce quadrillage qu’il se manifeste en profondeur, comme déjà là, attendant en silence le moment d’être énoncé. »

Pour provoquer chez nos petits la découverte, malgré leurs dissemblances, de la loi intérieure des choses, il faut, bien entendu, que nous leur permettions le plus grand nombre possible de découvertes (concrètes) des choses (d’où nécessité d’un environnement riche), mais il faut aussi que nous provoquions par notre écoute, par nos questions, par nos observations, l’exercice le plus fécond possible de leurs fonctions mentales (attention et logique) et l’expression de leurs constatations, de leurs démarches, de leurs découvertes (langage).

Car l’expérience n’enrichit l’homme (ou l’enfant) que dans la mesure où il sait en prendre conscience et la dominer.

Les prises de conscience fondamentales de l’enfant à l’école maternelle: prise de conscience de soi et de ses pouvoirs, et prise de conscience du milieu environnant, sont intimement liées: elles s’interpénètrent à travers toutes les situations vivantes dans lesquelles les enfants sont placés. À nous de provoquer ces situations et d’aider nos enfants à se les expliciter eux-mêmes. Il ne s’agit pas d’enseigner mais d’aider à découvrir, à analyser, à exprimer, à mettre à jour les prises de conscience du groupe enfantin, du milieu classe, du milieu école, du milieu familial, du milieu groupe social. De ne pas imposer la démarche adulte, mais de permettre aux enfants de classer avec ses propres critères, d’évaluer avec leurs propres mesures, de construire avec leurs propres moyens. Mais à l’occasion de ces classements, de ces évaluations, de ces constructions, de poser les bases d’un raisonnement logique, d’une réflexion élargie, dépassant peu à peu les bases strictement affectives du départ.

Exprimer mathématiquement les situations vécues par la classe, échanger les représentations graphiques enfantines avec celles de la classe correspondante et, de part et d’autre, «lire» ces graphes et reconstituer la situation vécue par d’autres enfants dans des temps et des lieux différents, n’est-ce pas la forme d’initiation mathématique qui répond le mieux à une pédagogie d’expression et de communication, à la pédagogie Freinet ?