|
Quand mathématiques et arts
se rencontrent et se répondent…
Créations mathématiques
Classe de CP, Ecole de Beaussais (Deux Sèvres). Enseignante, Catherine Tricoche
Cette année-là, je n'avais que 15 CP et je me sentais prête pour la méthode naturelle de mathématiques 1. J'ai donc commencé, avec ce groupe, les premières “ créations mathématiques ” 2. Je ne pensais pas aboutir aussi à l'Art !
"Vous allez faire une création mathématique avec des chiffres, des signes, ..."
(1) La méthode naturelle de math.
pratiquée dans une classe coopérative où l’expression peut jaillir librement, comporte différents axes possibles :
- les recherches math. A partir d’un événement, d’une situation…
- le travail d’entraînement en numération opération sur des fichiers autocorrectifs,
- le travail en géométrie,
- les créations math. (une démarche d’expression ouvrant sur une lecture du monde),
- les manipulations diverses (jeux à règles,...). |
|
| |
(2) Pour faire des créations mathématiques
Démarche : chaque enfant dispose d’une feuille blanche A4 et utilise un crayon qui laisse une trace plutôt foncée afin que la création soit bien lisible une fois affichée.
Consigne : vous allez faire une “ création mathématique ” (ou un “ texte mathématique ”) avec seulement des chiffres, des signes math., des points, des traits…
Durée : variable. De 5 à 20 minutes.
Puis toutes les créations sont affichées (en 2 x 2 groupes).
Les observateurs parlent d'une création puis, en dernier, l'auteur s'exprime à son tour. (démentant parfois complètement la vision des autres enfants).
Si l’effectif de la classe est important, on peut prévoir plusieurs moments dans la semaine pour regarder les créations et en parler. La phase de verbalisation est incontournable dans l’acte d’apprendre. |
|
Premières créations mathématiques
Chaque création est soumise à l'ensemble du groupe et chacun exprime ce qu’il découvre, en propose une lecture.
L'auteur donne sa “ version ”, son intention en dernier.
Découverte
A l'issue de cette première séance, ce sont surtout les créations de Flavie et de Aude qui marquent le groupe-classe à cause des symétries apparentes qui ont permis de détourner des chiffres de leur signification première…
Aude explique : C'est une étoile : 1 (en miroir) et 1, ça fait M, ε et 3 ça fait 8 (personne n'avait pratiqué cette lecture figurative !)
Flavie explique : un 6, un autre, estompés, yeux, trompe… j'ai fait presque un papillon !
Appropriation par les autres
Les enfants décident alors de refaire des créations math. En essayant le même principe que Aude et Flavie mais sans reprendre les mêmes chiffres… On est en plein tâtonnement.
Les résultats sont tout aussi intéressants et riches. Une lecture de la symétrie devient évidente avec la découverte de l’axe de symétrie.
Les enfants s'aperçoivent que certaines sont identiques “ à droite et à gauche du milieu, comme ça ” (main posée au milieu, perpendiculairement au tableau et séparant les 2 zones)… on plie à cet emplacement pour matérialiser la ligne séparant les deux zones et l'axe de symétrie est ainsi découvert par les enfants tout naturellement.
Je donne alors son nom et précise que dorénavant on utilisera ce terme “ symétrique ”.
|

Aude

Flavie, Un papillon, crayon estompé
|
|

Marc
|
On exerce
la découverte
Les enfants décident ensuite de plier leur feuille en 2 pour essayer à nouveau et faire des créations math “ bien symétriques ”…
|

Valentin
|
|

Clara
|
Nouveaux essais… On travaille sur la symétrie. On note les erreurs (chiffres non inversés, mal placés… ), on réessaye.
C'est alors qu'apparaît la création d'Alexis, étonnante de complexité, de perfection… bourrée de 5 et de 0 bien camouflés… époustouflante! |
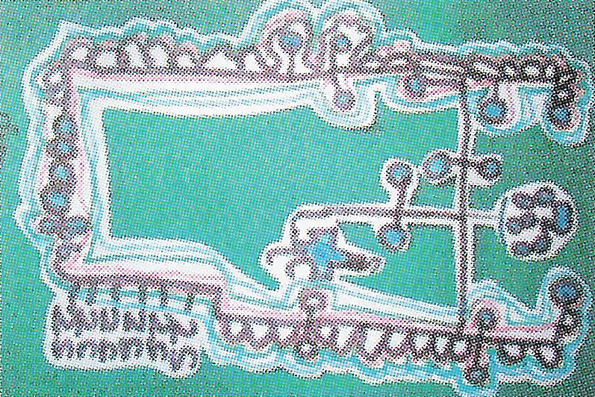
Clara
|
|

Flavie, insecte
|

Flavie
|

Tom
|
|
Une orientation nouvelle
Depuis le début de nos tâtonnements en Maths, beaucoup de productions m'avaient réellement interpellée. Pourquoi ces symétries centrales spontanées parfaites chez Aude ? (à 6 ans à peine !!!), comment?... D'où venait toute la “puissance” de certaines créations… Certaines ressemblaient à des mandalas, d'autres à des animaux, d'autres encore exprimaient quelque chose d'indicible et de très “ fort ” signes de l’expression singulière.
|

Jonathan
|

Aude
|
|

Alexis, Un moteur et des triangles
|
Sans aucun doute possible, certains enfants avaient déjà un pouvoir de créativité très “ développé ”. Tous, entraient facilement dans la création. Tous devaient pouvoir développer encore plus cette capacité de représentation de leur monde.
|

Jonathan
|
|