Les couleurs nous entourent de toutes part. Elles alimentent notre perception, nourrissent notre sensibilité au monde et forgent notre sens symbolique. Elles agissent directement sur l’affectif. Les mathématiques, quant à elles, favorisent la conceptualisation et le raisonnement logique (formulation d’hypothèses, vérifications). Elles sont davantage de l’ordre du conceptuel et du rationnel. Elles entrent dans notre vie par la voie de l’école et du travail. Existe – t - il cependant, et malgré ces apparentes oppositions, des liens entre « mathématiques de l’homme » et « couleurs du monde » ? Quels tissages pourrait-on créer ?

Récemment dans l’histoire de l’humanité, l’homme s’est servi indirectement des mathématiques pour modéliser des couleurs grâce à l’outil informatique. C’est donc que la production de couleurs artificielles a besoin de mathématiques.

Inversement, aujourd’hui, les mathématiques pourraient-elles avoir besoin des couleurs ? Par exemple, les concepts mathématiques pourraient-ils être davantage circonscrits et ainsi davantage compréhensibles grâce à une approche basée sur les couleurs ?

Un premier usage des couleurs en classe de mathématique est déjà celui des éditeurs scolaires qui proposent aux enfants du cycle 2 des exercices de « coloriage » utilisant un codage des couleurs. A chaque couleur est associé un nombre et il s’agit alors de calculer correctement des sommes pour trouver la couleur que l’éditeur a choisie pour chacune des parties (toutes juxtaposées) du dessin.

Rien de bien créatif jusqu’ici, l’intérêt étant pour l’enfant qu’un coloriage juste permette parfois de découvrir ce qui se cache derrière une multitude de traits et de chiffres comme dans le très ancien jeu des points liés.

Intersections de couleurs et résolutions de problèmes

Une autre piste est donnée par le concept d’intersection.

Si A et B sont deux ensembles, A inter B est l’intersection des deux, c’est l’ensemble des éléments qui appartiennent à la fois à A et à B ou encore, qui sont communs à A et B.

Si l’on examine la question de l’intersection de couleurs, on s’aperçoit que certaines couleurs ont quelque chose de commun. Par exemple, le vert et le violet ont le bleu cyan en commun dans le cadre de couleurs lumière (RVB primaires). On se heurte cependant ici à un obstacle car le bleu ne peut pas être désolidarisé du jaune dans le vert ni du rouge dans le violet sans que le vert ou le violet ne perdent leur identité. Cette notion d’intersection trouve donc ici ses limites.

Cette difficulté peut cependant être contournée en définissant l’intersection de couleurs comme la superposition de deux ensembles qui s’interpénètrent ou se mélangent (définition de la couleur matière CMJ). Dans ces conditions, le jaune (A) et le bleu (B) donneraient le vert (A inter B).

Pour amener l’enfant à une démarche de résolution de problème, certaines couleurs peuvent être « effacées » (il suffit pour cela de photocopier un graphisme et de ne reporter que certaines couleurs). L’enfant aura alors à formuler des hypothèses qu’il lui faudra dans un second temps apprendre à vérifier grâce à un matériel approprié (crayons de couleur, peinture etc.) puis, à prouver (en se passant de tout matériel justement) en se basant sur des règles de mélange maintes fois vérifiées par tâtonnement et ainsi institutionnalisées dans la classe (processus d’appropriation).

La tâche problématique serait alors ainsi formulée « Comment obtenir une couleur donnée ? ». Dans le même esprit que les Sudoku japonais, qui sont d’autant plus difficiles à résoudre que le format des tableaux est grand, lorsque les mélanges de couleurs sont nombreux et complexes, retrouver la couleur d’origine de certains ensembles (délimités par une ligne fermée) peut devenir également un véritable casse tête.

Par exemple, comment, dans les figures ci-contre (où seules certaines couleurs originales auraient été reportées) pouvoir retrouver la couleur (couleur matière, CMJ) de chacun des ensembles non colorés ?

Le premier cas est assez simple : à quelle couleur ajoute-t-on du jaune pour avoir de l’orange ? Le rouge vient vite à l’esprit

Le deuxième cas est plus élaboré car des « nuances de couleurs » apparaissent. C’est ainsi que les deux verts obtenus sur l’ovale jaune ne peuvent l’être que par des bleus de ton différents, couleurs de l’ovale vertical et du polygone de gauche. On trouve de même que les deux autres ovales horizontaux ne peuvent être que rouges.

On se rapproche à cet égard de démarches (de type scientifique) fréquemment utilisées en mathématiques puisque certains choix de couleurs peuvent conduire à des contradictions et donc à des impasses, ce qui impose de modifier les hypothèses formulées, etc.

La question de l’éventuelle mathématisation d’un tel modèle de recherches de couleurs peut se faire dans un second temps, en associant simplement à chaque couleur un nombre avec une « règle » supplémentaire qui précise alors à quoi un mélange de couleurs correspondrait au niveau mathématique.

La production d'un élève après que le processus de traduction des couleurs en nombre et puissance ait été mis en évidence en classe entière.

Commutativité/associativité

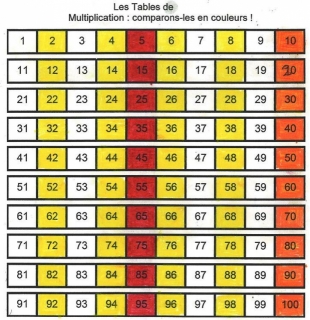
Il en résulte alors un certain nombre de principes que l’action mathématique correspondant au mélange de couleurs devrait vérifier. Cette action doit être commutative. En effet, mélanger du bleu et du jaune ou du jaune et du bleu est équivalent. Cette action doit être associative. En effet, lorsque je mélange trois couleurs, je peux en mélanger deux puis ajouter la troisième ou bien mélanger les trois en même temps.

Arrêtons-nous là ! : l’addition et la multiplication semblent déjà toutes deux convenir. Cependant, il n’est pas difficile de se rendre compte que la multiplication convient ici davantage que l’addition. Imaginons en effet que l’addition convienne. Le nombre 6 représenterait alors une couleur qui puisse être obtenue à l’aide des mélanges de 5 et 1, de 4 et 2 ou de 3 et 3. La couleur du 6 serait le résultat de mélanges divers pouvant être obtenus avec les couleurs des nombres 1, 2, 3, 4, 5 et 6. En généralisant, toute couleur (codée par un nombre n) « contiendrait » toutes les couleurs la précédant (n-1, n-2,…/… 2, 1) : on ne pourrait alors, et par exemple, jamais obtenir deux des trois couleurs primaires, ce qui ne nous conviendrait pas.

La multiplication en revanche permet de garder une trace des nombres (et donc des couleurs) par lesquels elle se réalise via une certaine forme de codage.

Ainsi, si on associe au jaune le nombre 2, au bleu le nombre 3 et au rouge le nombre 5, on obtient un système de représentation des couleurs permettant d’obtenir tout le cercle chromatique en considérant les multiples de 2 (contiennent au moins une couche de jaune), de 2m (contiennent davantage de jaune), de 3 etc.

La question de l’utilité d’une telle mathématisation du graphisme coloré se pose alors.

Nous laissons au lecteur le soin de réfléchir à toutes les possibilités offertes par un « milieu » où nombres et couleurs seraient tout autant régis par les règles de la chromatique que par celles de l’arithmétique PGCD (plus grand commun diviseur) et PPCM (plus petit commun multiple) ; notamment voir ci-après. Cela permettrait - il aux enfants de mieux comprendre les couleurs ? Les nombres ? les deux ? aucun des deux ?

En réponse à l’analyse du deuxième cas (ci - avant), on peut émettre l’hypothèse que le domaine numérique permet une discrimination plus fine des couleurs, évitant ainsi de fastidieuses recherches de couleurs.

La table de Pythagore (et ses variantes) donne d’ailleurs une clé de passage des nombres aux couleurs et inversement (coloriée comme ci - dessus dès septembre 2001, dans une classe coopérative de CE2, à Marseille).

Lisa et Garance réussissent une distinction non équivoque (séparation complète des couleurs et distinction entre les différentes puissances comme autant de bandes d'une même couleur).

On peut montrer que, finalement, il suffit de considérer les nombres (2m x 3n x 5p).pour obtenir toutes les couleurs du cercle chromatique. Inversement, on remarque alors que l’on ne peut pas atteindre tous les nombres entiers naturels par une telle modélisation. Pensez à 7 par exemple !

A cet égard, parler de la décomposition de couleurs en couleurs de bases se transpose mathématiquement au niveau du codage d’un nombre par les nombres premiers. L’unicité d’une couleur obtenue à partir des mêmes quantités de peintures de base coïncide alors au niveau mathématique à l’unicité de la décomposition en facteurs premiers des entiers naturels.

Par exemple, il existe trois façons de mélanger deux doses de bleu (32) et une dose de jaune (21) : tout est mélangé en même temps (18x1 ou 1x18), les deux doses de bleu (32) sont associées à la dose de jaune (21) ou encore, une dose de bleu et une dose de jaune sont d’abord associées (3x2) puis sont mélangés à une dose de bleu.

On retrouve bien les différentes décompositions de 18 en produit de deux facteurs (18 = 18x1 = 9x2 = 6x3) et il y a concordance entre l’unicité de coloration du mélange final (quelque soit l’ordre de mélange) et l’unicité de décomposition de 18 en facteurs premiers élevé de leur puissance (18 =21 x 32 ).

Se réconcilier avec les mathématiques

Il est alors possible d’exploiter un tel système dans des activités très variées et de tout âge, à tout moment. Une telle démarche peut aider à concilier ou à réconcilier les enfants avec les mathématiques d’une part et avec la résolution de problème d’autre part, celle-ci étant trop souvent considérée comme l’apanage des mathématiques, dont elle ne constitue, encore aujourd’hui, pourtant pas assez souvent le cœur.

On propose ci-après deux exemples (figures a et b) à résoudre mathématiquement et/ou par une recherche de couleurs (cas valorisant les points de vue symétriques de PGCD et PPCM ainsi que deux autres (figures c et d) qui peuvent être à « mathématiser ».

- la figure (c) est « résolue » en couleurs.

- La figure (d) peut avoir la figure (c) comme solution mais possède une autre solution en couleurs et donc une autre solution mathématisée (que nous laissons à la sagacité du lecteur).

Une question mérite ici d’être posée : la mathématisation des couleurs peut-elle favoriser une coloration des mathématiques ?

sommaire "Arts et maths"